加个权吧
前面说的是均匀抽样,要是想加个权怎么办呢?先说加权有什么用呢?比如我们已经统计好了搜索的关键字和词频,那么有了加权就可以直接用这个数据来抽样而无需把关键字重复好多遍了。
我们先来看看这个抽样应该是怎么样的。假设这总共 $n$ 项都摆在你面前了,设第 $i$ 项的权值为 $w_i$,那么我们抽到这一项概率应该是
$$P_i = \frac{w_i}{w_1 + w_2 + \cdots + w_n}$$
我们现在来看看,如果把这 $n$ 项按照第 $n$ 项、第 $n-1$ 项、…… 第 $2$ 项、第 $1$ 项的顺序抽出来,这个概率是多少。因为这 $n$ 项的顺序是可以随便摆的,所以它求出来是有一定普遍意义的。
第一次抽出第 $n$ 项的概率是
$$P_n(1) = \frac{w_n}{w_1 + w_2 + \cdots + w_n}$$
第 $n$ 项已经被抽走了,那第二次抽到第 $n-1$ 项的概率是
$$P_{n-1}(2) = \frac{w_{n-1}}{w_1 + w_2 + \cdots + w_{n-1}}$$
以此类推,按照这个顺序抽出所有元素的概率就是
$$P(S) = \prod_{i=1}^n \frac{w_i}{w_1+w_2+\cdots w_i} $$
这有什么用呢?别着急,先记下这个结果,我们下面来说说算法怎么做。
其实这个算法简单得不能再简单了——还记得第 1 讲里面说的那个给每个数标上一个随机数的方法吗?这次只需要给生成的随机数 $U_i$ 上面加一个方次变成 $U_i^{1/w_i}$ 就好了。记得 $U_i$ 是在 $[0,1]$ 之间的,所以 $w_i$ 越大,这个随机数就放得越大,也就越容易挤进堆里面了。程序如下:
def reservoirSampleAES(stream, sample_size):
result = []
for index, line in enumerate(stream):
w = (index + 1)** (1/2)
key = random.random() ** (1/w)
if index < sample_size:
heapq.heappush(result, (key, line))
elif key > heapq.nsmallest(1, result)[0][0]:
heapq.heappushpop(result, (key, line))
return list(zip(*result))[1]
这里我们取的权值是序号的开方,效果如何呢?我做了这样一个仿真:
import matplotlib.pyplot as plt
a = []
for i in range(10000):
a.extend(reservoirSample(range(100), 10))
plt.hist(a, 100)
plt.show()
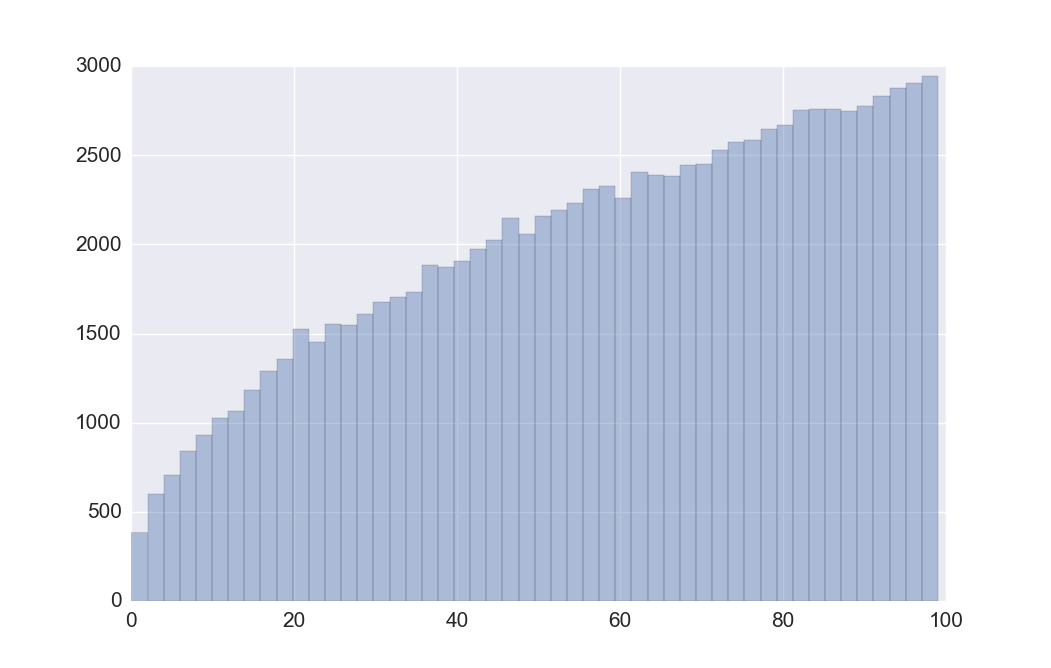
还挺像那么回事的哈。再回过头来看看这个算法是什么道理。我们现在要证明的就是,既然 $U_i$ 都是 $[0,1]$ 上均匀分布的随机数,$w_i$ 是权值,那么以特定顺序排列 $X_i = U_i ^{1/w_i}$ 的概率和前面说的加权抽取一样:
$$\mathbb{P}[X_1 \leq X_2 \leq \cdots \leq X_n \leq 1] = \prod_{i=1}^n \frac{w_i}{w_1+w_2+\cdots w_i} $$
这个还得来数学归纳法…… 首先,对于 $t \in [0,1]$,$w_i > 0$,分布函数
$$F_{X_i}(t) = \mathbb{P}[X_i \leq t] = \mathbb{P}\big[ U_i^{1/w_i}\leq t\big] = \mathbb{P}\big[U_i \leq t^{w_i}\big] = t^{w_i}$$
那么概率密度函数
$$f_{X_i}(t) = F_{X_i}'(t) = w_i\cdot t^{w_i -1}$$
$n=1$ 时,$\mathbb{P}[U_1 \leq \alpha^{w_1}] = \alpha^{w_1}$
$n=2$ 时,
$$\begin{align}
\mathbb{P}[U_1 \leq U_2 \leq \alpha^{w_1}] &= \int_0^\alpha F_{X_1}(t)\,f_{X_2}(t) \mathrm{d}t\\
&=\int_0^\alpha t^{w_1}\cdot w_2 t^{w_2-1}\mathrm{d}t = \frac{w_2}{w_1 + w_2}\cdot \alpha^{w_1+w_2}
\end{align}$$
那么如果 $n=k$ 时,$$\mathbb{P}[X_1 \leq X_2 \leq \cdots \leq X_k \leq \alpha] = \alpha^{\sum_{i=1}^k w_i}\prod_{i=1}^k \frac{w_i}{w_1+w_2+\cdots w_i} $$
则 $n=k+1$ 时,
$$\begin{align}
&\phantom{==} \mathbb{P}[X_1 \leq X_2 \leq \cdots \leq X_{k+1} \leq \alpha] \\
&= \int_0^\alpha \mathbb{P}[X_1 \leq X_2 \leq \cdots \leq X_k \leq t]\cdot f_{X_{k+1}}(t) \mathrm{d}t\\
&=\int_0^\alpha \left(\prod_{i=1}^k \frac{w_i}{w_1+w_2+\cdots w_i}\right) t^{\sum_{i=1}^k w_i}\cdot w_{k+1} t^{w_{k+1}-1}\mathrm{d}t \\
&= \left(\prod_{i=1}^k \frac{w_i}{w_1+w_2+\cdots w_i}\right)w_{k+1} \int_0^\alpha t^{\sum_{i=1}^{k+1} w_i-1}\mathrm{d}t \\
&=\alpha^{\sum_{i=1}^{k+1} w_i}\prod_{i=1}^{k+1} \frac{w_i}{w_1+w_2+\cdots w_i}
\end{align}$$
$\alpha = 1$ 的时候前面那一项就没有了,所以对于任意元素排列,用 $U_i^{1/w_i}$ 方法得到它的概率和直接加权抽取得到的概率是一样的。这样就证明了这个方法是可行的。
虽然证明看起来啰嗦了点,但是不得不说这个结果简单优雅,真的太精到了。以前虽然也有一些加权抽样的算法,但是都不能像这个实现未知总数时的线上抽样。直到 2005 年这个算法才被提出来。
Cloudera 的机器学习项目 Oryx 里面就应用了这个加权抽样算法,代码可以看这里。当然它写的是对随机数取对数再除以权值,这个算起来当然是比直接开 $w_i$ 次方要快一点啦。
参考资料
- Efraimidis, Pavlos S., and Paul G. Spirakis. “Weighted random sampling with a reservoir.” Information Processing Letters 97.5 (2006): 181-185.
更多算法内容请见《算法拾珠》。
