Sorry, this entry is only available in 中文.
Month: September 2012
What kind of food scale do we really want?

Least Error Cartesian Meshing
This is actually the Project Euler problem of last week – I know it’s not good to post the answer of new problems here, but this is indeed a very intriguing problem. In short, the problem is as follows: Given a unit circle within radius of 1, we try to represent it by non-uniform mesh. N lines are inserted into the square [-1, 1] x [-1, 1]. Cells are colored red if they overlap with the unit circle, black otherwise. Find the way to make the red area minimum. Here is my solution on N = 16. 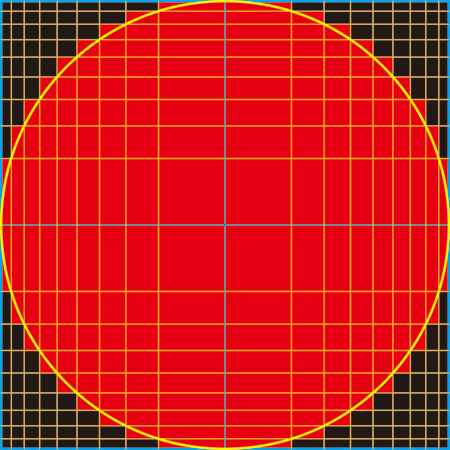 Continue reading “Least Error Cartesian Meshing”
Continue reading “Least Error Cartesian Meshing”
