哪能搞法——分支界限
我们先把动态规划的想法放一下,退一步来看看这个问题。每一个物品都可能放或者不放,如果用一个决策树来表示的话,就得到这样一棵满二叉树:
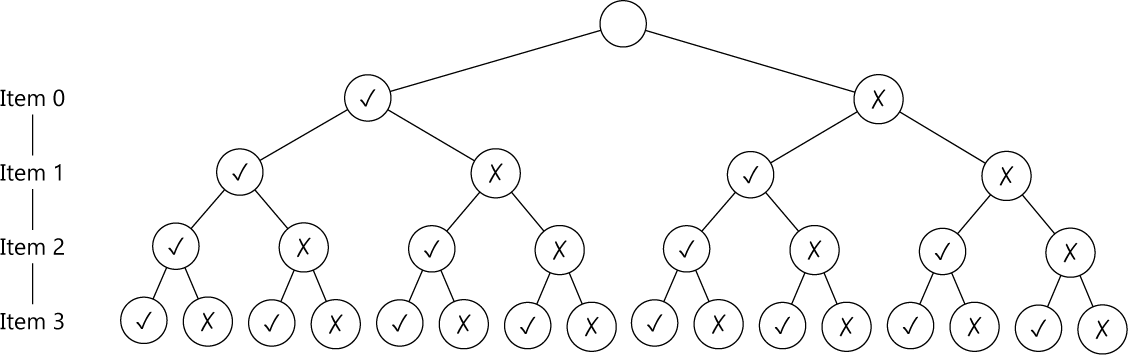
这对于 \(n\) 个物品就有 \(2^n\) 种放法,总共要计算 \(2^{n+1} – 2\) 个结点,当然是太多了。不过,有没有什么办法能让遍历的结点少一点呢?
比较直观的,至少有这么两个:
- 重量超限的——如果一个结点重量超限,那再往上加东西的也不用看了。
- 最下面一层的右侧打叉的结点——结果肯定和上一层一样,也不用再算一遍了。
还有吗?比如说,有些结点重量大而价值却很低,再怎么往上加东西也没有竞争力,能不能尽早找出这种“没有希望”的结点呢?
对于一些固定的物品,包包里能装走的价值是有一个上限的。包的大小是一定的,那么为了让总体价值最大,就要让单位重量的价值最大。怎么才能让单位重量的价值最大呢?我们把所有的物品按照价值与重量的比值(\(v_j / w_j\))由大到小排序,先尽量拣着重量小价值大的东西装,而把又重又不值钱的放在后面。
最后包包还没装满又放不下下一个物品怎么办呢?那我们就假装这个物品可以切开,然后把包包塞满。这样一来,现在得到的这个总价值就是一个上限,因为单位价值最高的那些已经都塞进来啦。
我们把物品排好顺序挨个考虑,如果有个结点已经考虑了前 \(i\) 个物品,得到的总价值是 \(V_0\),总重量是 \(W_0\);我们按照单位价值从大到小挨个往里放,放到第 \(k\) 个物品放不下了,这时候包里的总重量是
\[
\tilde{W} = W_0 + \sum_{j=i+1}^{k-1} w_j
\]
而总价值的上限就是
\[
V_{\rm bound} = \left(V_0 + \sum_{j=i+1}^{k-1} v_j \right) + \big(W – \tilde{W}\big)\cdot \frac{v_k}{w_k}
\]
其中前面一项是放进去的物品总价值,后面一项是把第 \(k\) 个物品切开后塞满包包的价值。
如果用 \(V_{\max}\) 表示已经出现过的最高价值,那遇到 \(V_{\rm bound} \leq V_{\max}\) 的结点就可以直接把它剪掉啦。
这个程序写出来可以是这样的:
import sys
def knapsack(vw, limit):
def bound(v, w, j):
if j >= len(vw) or w > limit:
return -1
else:
while j < len(vw) and w + vw[j][1] <= limit:
v, w, j = v + vw[j][0], w + vw[j][1], j + 1
if j < len(vw):
v += (limit - w) * vw[j][0] / (vw[j][1] * 1.0)
return v
def traverse(v, w, j):
nonlocal maxValue
if bound(v, w, j) >= maxValue: # promising
if w + vw[j][1] <= limit: # w/ j
maxValue = max(maxValue, v + vw[j][0])
traverse(v + vw[j][0], w + vw[j][1], j + 1)
if j < len(vw) - 1: # w/o j
traverse(v, w, j + 1)
return
maxValue = 0
traverse(0, 0, 0)
return maxValue
if __name__ == "__main__":
with open(sys.argv[1] if len(sys.argv) > 1 else sys.exit(1)) as f:
limit, n = map(int, f.readline().split())
vw = [] # value, weight, value density
for ln in f.readlines():
vl, wl = tuple(map(int, ln.split()))
vw.append([vl, wl, vl / (wl * 1.0)])
print(knapsack(sorted(vw, key=lambda x : x[2], reverse=True), limit))
简单解释一下,先对 vw 按照单位重量的价值排序,然后利用 bound 函数确定价值上限。如果价值上限超过了已经出现的最大价值,再分别计算加上当前物品和不加当前物品的两种情况,否则就跳过。
我们还拿前面的那个小例子来看,它执行过程可以用下面这个图来表示:
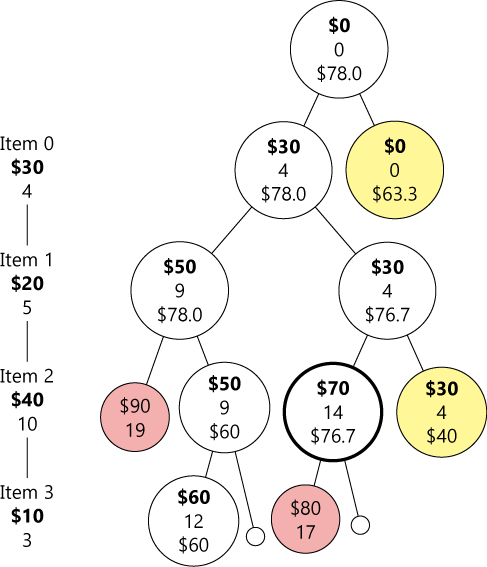
显然这是一个深度优先搜索,图中每个结点分别列出了它的当前价值、当前重量和价值上限,红色结点表示重量超限,黄色结点表示价值上限不足,加粗的圈是最优解。这个树看起来比上面那个小多了吧!
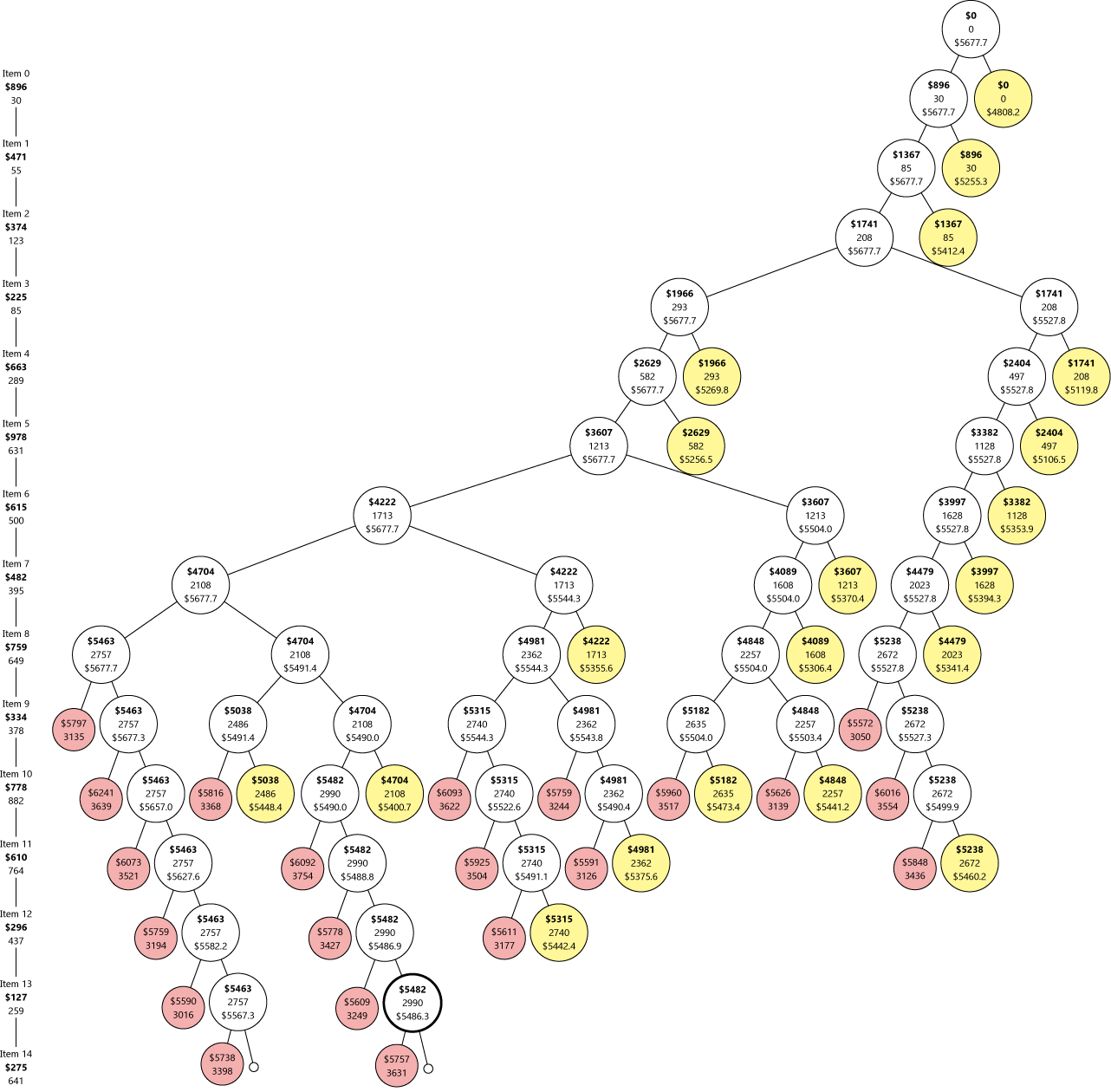
如果包包大一点,效果就更明显了,比如这个有 15 个物品的包包,它的搜索过程是这样的(点击看大图):
看看我们剪掉了多少红圈黄圈!看起来很不错,让我们来试试前面的那些大包包…… 诶怎么回事……
RuntimeError: maximum recursion depth exceeded while calling a Python object
好吧递归太深了……我们可以加大递归深度:
import thread
...
def main():
...
if __name__ == "__main__":
threading.stack_size(67108864) # 64MB stack
sys.setrecursionlimit(20000)
thread = threading.Thread(target=main)
thread.start()
在 Windows 下面递归深度除了受 recursion limit 约束,还受栈空间限制,所以这里用 thread 来设定栈空间,而它只对新建的线程有效。如果不扩大栈空间,2000 个项目还可以,10000 个就不行了。
当然,所有的递归都是可以解开的,为什么非要用递归呢!直接把后面待处理的结点压进栈里不就行了吗,当然要注意压栈的顺序变了:
def knapsack(vw, limit):
def bound(v, w, j):
...
maxValue = 0
stack = [[0, 0, 0]] # value, weight, index
while stack:
v, w, j = stack.pop()
if bound(v, w, j) >= maxValue:
if j < len(vw) - 1:
stack.append([v, w, j + 1])
if w + vw[j][1] <= limit:
maxValue = max(maxValue, v + vw[j][0])
stack.append([v + vw[j][0], w + vw[j][1], j + 1])
return maxValue
那个有 10000 个元素的大包包也完全不在话下,瞬间就可以解开啦!
更多算法内容请见《算法拾珠》。

One thought on “0-1 背包问题详解 (3)”