这个实际上是上个星期的 Project Euler 题目——我也知道贴答案不好,但是这个问题实在很有意思:给定一个单位圆,在 [-1, 1] x [-1, 1] 里面插入 N 条线,如果小单元和单位圆重叠就标为红色,否则标为黑色。找出让红色区域最小的划分方法。我在 N = 16 时候的解是这个样子的: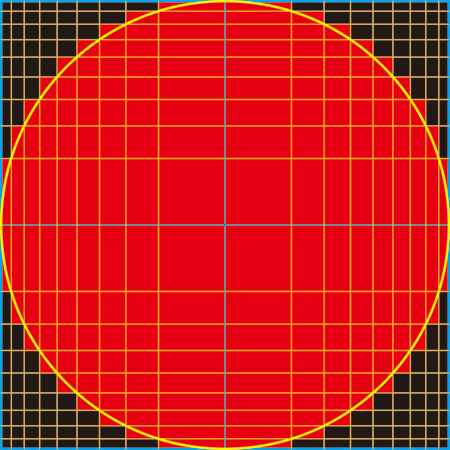 我还没查现有的文献,但是这应该是个很实际的问题,比如做自适应网格仿真的时候,这种减小误差的方法就有意义了。很显然这个圆是对称的。我们就只要看第一象限就好了。令 \(n = \frac{1}{2} N\),那么这里 \(n = 8\)。我们还知道 \(x_0 = 0, x_{n+1} = 1\)。
我还没查现有的文献,但是这应该是个很实际的问题,比如做自适应网格仿真的时候,这种减小误差的方法就有意义了。很显然这个圆是对称的。我们就只要看第一象限就好了。令 \(n = \frac{1}{2} N\),那么这里 \(n = 8\)。我们还知道 \(x_0 = 0, x_{n+1} = 1\)。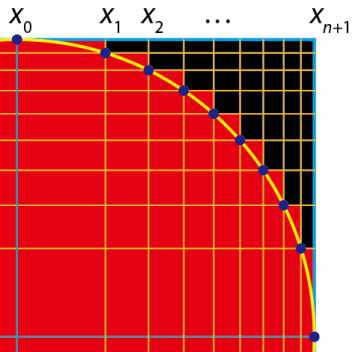 为了让覆盖的网格数最小,很显然格点需要落在圆上。于是对于任意一点来说,\(x_i^2+y_i^2 = 1\)。易知面积
为了让覆盖的网格数最小,很显然格点需要落在圆上。于是对于任意一点来说,\(x_i^2+y_i^2 = 1\)。易知面积
\[
S= (x_1-x_0)\cdot y_0 + (x_2-x_1)\cdot y_1 + \cdots + (x_{n+1}-x_n)\cdot y_n).
\]
最后选出的每个格点都是最优的,也就是说,一条竖线不管是往左还是往右移动,\(S\) 都会增加,于是 \(S\) 对 \(x_i\) 的偏导数
\[
\begin{aligned} \displaystyle \frac{\partial S}{\partial x_i} &= \frac{\partial \big[ (x_i-x_{i-1})\cdot y_{i-1} + (x_{i+1}-x_i)\cdot y_i )\big]}{\partial x_i} \\
&=\displaystyle y_{i-1}-y_i+(x_{i+1}-x_i)\frac{\partial y_i}{\partial x_i}\\
&=\displaystyle y_{i-1}-y_i-(x_{i+1}-x_i)\frac{x_i}{\sqrt{1- x_i^2}}\\
&=\displaystyle y_{i-1}-y_i-(x_{i+1}-x_i)\frac{x_i}{y_i} \end{aligned}
\]
必须为零。因此
\[
\displaystyle x_{i+1} = \frac{x_i^2-y_i^2+y_{i-1}y_i}{x_i}.
\]
有了这个递推关系,一旦选好了 \(x_1\),剩下的位置就都确定了,如果算到 \(x_{n+1}\) 正好等于 1,那就算大功告成。很不幸的是,我没看出来有什么简便的方法可以直接解出 \(x_i\)。于是就随便选一个 \(x_1\) 的初值,然后用数值方法优化找到 \(S\) 的极值。当然,如果 \(x_1\) 选得太靠右,可能算到一半就发现有些点落到方框之外了。
Python 实现:
from __future__ import division
from math import sqrt
N = 16 / 2
def S(x1):
x = [0 for _ in xrange(0,N+1)]
y = [0 for _ in xrange(0,N+1)]
s = x[1] = x1
y[1] = sqrt(1-x[1]**2)
y[0] = 1
for i in xrange (2,N+1):
x[i] = (2 * x[i-1]**2 - 1 + y[i-1] * y[i-2]) / x[i-1]
if x[i] >= 1:
return 100
y[i] = sqrt(1 - x[i]**2)
s += (x[i] - x[i-1]) * y[i-1]
s += (1 - x[i]) * y[i]
return s * 4
step = a = 1 / N # Search for the optimal x1 = a
while step > 10 ** (-11):
if S(a + step) > S(a):
a -= step
step /= 10
print a, S(a)
else:
a += step
这样就得到了结果,N=16 时覆盖的面积是 3.2841361679。如果 N 增大到 100,覆盖的面积就缩小到 3.16896916573。
我还是试图想找到一个闭式表达,但是没有结果。把 \(x_i\) 画成图用多项式去拟合,结果还不错,但是也没有找到一个方法好直接确定参数。先这么着吧。

你可以把代码移除吗? 任何人都可以搜寻到你的文章,,用这里的代码得到答案,这样等于让人作弊, 希望你可以把他移除, 谢谢