Least Error Cartesian Meshing

This is actually the Project Euler problem of last week – I know it’s not good to post the answer of new problems here, but this is indeed a very intriguing problem. In short, the problem is as follows: Given a unit circle within radius of 1, we try to represent it by non-uniform mesh. N lines are inserted into the square [-1, 1] x [-1, 1]. Cells are colored red if they overlap with the unit circle, black otherwise. Find the way to make the red area minimum. Here is my solution on N = 16. 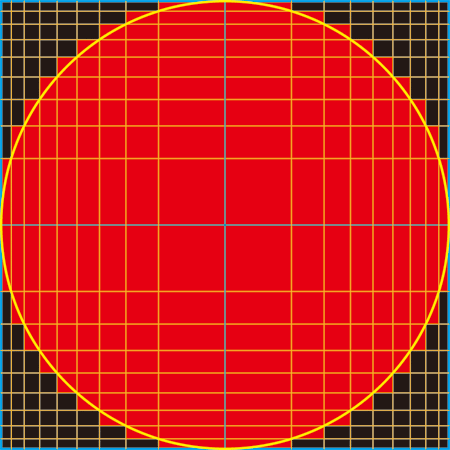I haven’t done the research on existing literature though, but this would be a very practical problem, which might be useful on simulation with adaptive meshing. Because of the obvious symmetry, we are only looking at the first quadrant. Let \(n = \frac{1}{2} N\), so here in this example, \(n = 8\). Also we know that \(x_0 = 0, x_{n+1} = 1\). 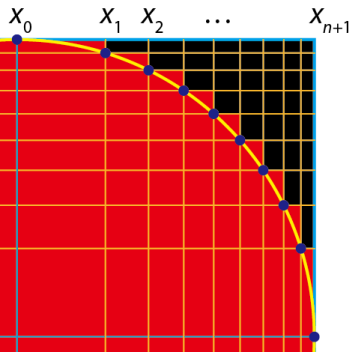To minimize the number of cells covered, the grids have to fall on the unit circle. Therefore, \(x_i^2+y_i^2 = 1\) for any point \(i = 1, 2, \ldots, n\). It is clear that the area
\[
S= (x_1-x_0)\cdot y_0 + (x_2-x_1)\cdot y_1 + \cdots + (x_{n+1}-x_n)\cdot y_n).
\]

Our position of each grid has to be optimal, that is, if any grid point moves to the left or right, \(S\) will increase. So the partial derivative of \(S\) with respect of \(x_i\)

\[
\begin{aligned} \displaystyle \frac{\partial S}{\partial x_i} &= \frac{\partial \big[ (x_i-x_{i-1})\cdot y_{i-1} + (x_{i+1}-x_i)\cdot y_i )\big]}{\partial x_i} \\
&=\displaystyle y_{i-1}-y_i+(x_{i+1}-x_i)\frac{\partial y_i}{\partial x_i}\\
&=\displaystyle y_{i-1}-y_i-(x_{i+1}-x_i)\frac{x_i}{\sqrt{1- x_i^2}}\\
&=\displaystyle y_{i-1}-y_i-(x_{i+1}-x_i)\frac{x_i}{y_i} \end{aligned}
\] has to be zero. Therefore
\[
\displaystyle x_{i+1} = \frac{x_i^2-y_i^2+y_{i-1}y_i}{x_i}.
\]

Once we select the position \(x_1\), all the rest can be derived out of this. With a given \(n\), if \(x_{n+1} = 1\), then we’ve found our solution. Unfortunately, I don’t see any easy way of solving this. So I just randomly pick an \(x_1\), and try to numerically find the extreme value of \(S\). Of course, if you move \(x_1\) too far to the right, some following points may fall out of the range.

My Python implementation:

from __future__ import division
from math import sqrt
N = 16 / 2

def S(x1):
    x = [0 for _ in xrange(0,N+1)]
    y = [0 for _ in xrange(0,N+1)]
    s = x[1] = x1
    y[1] = sqrt(1-x[1]**2)
    y[0] = 1
    for i in xrange (2,N+1):
        x[i] = (2 * x[i-1]**2 - 1 + y[i-1] * y[i-2]) / x[i-1]
        if x[i] >= 1:
            return 100
        y[i] = sqrt(1 - x[i]**2)
        s += (x[i] - x[i-1]) * y[i-1]
    s += (1 - x[i]) * y[i]
    return s * 4

step = a = 1 / N                # Search for the optimal x1 = a
while step > 10 ** (-11):
    if S(a + step) > S(a):
        a -= step
        step /= 10
        print a, S(a)
    else:
        a += step

Then I got my result and the area of my cells covered is 3.2841361679, for N=16. When N=100, our covered area is 3.16896916573.

I actually tried to get closed-form formula of \(x_i\), but to no avail. Although they fit pretty well to polynomials, it can hardly be convincing. I’ll just leave it for now.