这个元旦过的颇不宁静。前阵子看到一篇讲“可以喝的书”的文章火爆微博,觉得是个有点意思的想法,并没有太在意。不想过了两日,朋友圈转出一篇微博文章《如何评价外国女生发明的可以喝的书(The Drinkable Book)?》,当时和老婆讨论了下,觉得作者将其斥为忽悠太过武断,但也不过一家之言尔。不料又过了一日,这篇漏洞百出的文章居然被多家媒体转载,阅读量数百万,标题也变成了《鸡汤有毒!刷爆朋友圈的“可以喝的书”是假的》,简直已经盖棺定论。追根溯源,这篇第一高票回答在知乎这个所谓的知识社区竟获得近四千赞,作者修改回答后的口吻也愈发不容置疑,而知乎竟以“不友善”为由删除了一些反对评论。及至此时,方觉此种言论威力之大,流毒之广,不能不说点什么了。
Continue reading “毒喊捉毒的反鸡汤”
作者: 犊犊
正态分布随机数的生成 (2)
没有看过上一篇的同学请看正态分布随机数的生成 (1)。
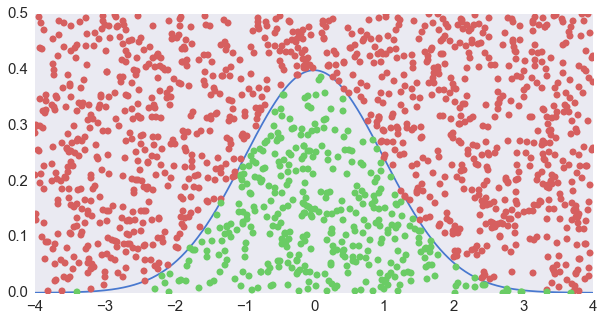
接受—拒绝法
求反变换固然还可行,但是碰到无法解析求逆的函数,用数值方法总归比较慢。下面我们就来说说另一个能够适合任何概率密度分布的方法——接受—拒绝法 (Acceptance-Rejection Method),国内也有翻译成叫做舍选法的。接受—拒绝法的思路其实很简单——比如说你想要正态分布,我们就弄个方框框把它框起来,然后均匀地往里面扔飞镖。扔到曲线以下我就留着,扔到曲线以上就不要了。这样搞好以后来看,曲线之下的点就是(二维)均匀分布的。那这些点的横坐标就正好满足我们要的分布——高的地方的点就多,低的地方的点就少嘛。
VMware Player 升级 / 卸载报错
我今天试图卸载 VMware player 7.1.2 – 结果它蹦出来一个错
The MSI '' failed
这到底什么意思…… VMWare 给了一个 KB 文章 kb.vmware.com/kb/1031302,不过……基本上什么也没说。看看那 500 多个 1 星打分就知道了。
正态分布随机数的生成 (1)
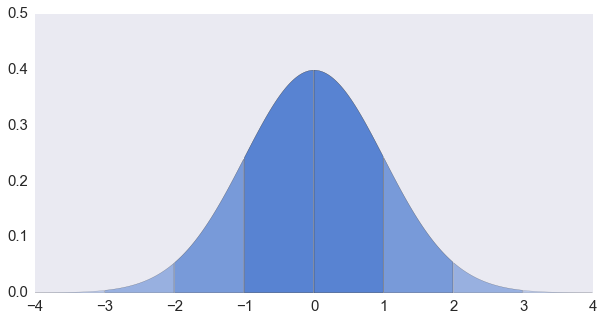
正态分布——听起来非常耳熟,用起来也很顺手——因为很多语言都已经内置了有关正态分布的各种工具。但其实,在这个最普遍、最广泛的正态分布背后,要生成它还有很多学问呢。
$$f(x \; | \; \mu, \sigma) = \frac{1}{\sigma\sqrt{2\pi} } \; e^{ -\frac{(x-\mu)^2}{2\sigma^2} }$$
难道教科书上没有讲吗?看看概率书上是怎么说的……比如我手头这本浙大版的《概率论与数理统计》(第四版)第 378 页上说……“标准正态变量的分布函数 $\Phi(x)$ 的反函数不存在显式,故不能用逆变换法产生标准正态变量……”
Continue reading “正态分布随机数的生成 (1)”
蓄水池抽样浅说 (3)
加个权吧
前面说的是均匀抽样,要是想加个权怎么办呢?先说加权有什么用呢?比如我们已经统计好了搜索的关键字和词频,那么有了加权就可以直接用这个数据来抽样而无需把关键字重复好多遍了。
我们先来看看这个抽样应该是怎么样的。假设这总共 $n$ 项都摆在你面前了,设第 $i$ 项的权值为 $w_i$,那么我们抽到这一项概率应该是
$$P_i = \frac{w_i}{w_1 + w_2 + \cdots + w_n}$$
我们现在来看看,如果把这 $n$ 项按照第 $n$ 项、第 $n-1$ 项、…… 第 $2$ 项、第 $1$ 项的顺序抽出来,这个概率是多少。因为这 $n$ 项的顺序是可以随便摆的,所以它求出来是有一定普遍意义的。
第一次抽出第 $n$ 项的概率是
$$P_n(1) = \frac{w_n}{w_1 + w_2 + \cdots + w_n}$$
第 $n$ 项已经被抽走了,那第二次抽到第 $n-1$ 项的概率是
$$P_{n-1}(2) = \frac{w_{n-1}}{w_1 + w_2 + \cdots + w_{n-1}}$$
以此类推,按照这个顺序抽出所有元素的概率就是
$$P(S) = \prod_{i=1}^n \frac{w_i}{w_1+w_2+\cdots w_i} $$
这有什么用呢?别着急,先记下这个结果,我们下面来说说算法怎么做。
蓄水池抽样浅说 (2)
没有看过前一篇的同学请看这里:蓄水池抽样浅说 (1)
跳跳跳!—— Algorithm X
前面介绍的方法都很好,但是要计算 $n-k$ 个随机数实在是有点浪费时间…… 有兴趣的同学可以把那个调用函数换成比如 reservoirSample(range(10**8), 10**5),就知道这东西还是要算上一会儿的了。
再来看看这个过程吧——把前 $k$ 个元素放进去之后,随机决定接下来的元素要不要放进去,但是每次决定时都需要产生一个随机数。要是我们能够确定应该跳过多少个元素,不就可以省掉很多生成随机数的工夫了吗?每一步过程就变成了
- 确定该跳过多少个元素 $S(k, n)$
- 跳过 $S(k, n)$ 个元素
- 从前 $k$ 个元素中随机产生一个要替换的元素,用下一个元素替换
蓄水池抽样浅说 (1)

我们有时候会有进行数据抽样的需要,比如要从文件中随机取出若干行,或从数据集中随机取出若干数据进行分析。通常情况下这并不是什么难事,比如 Python 中直接提供了 random.sample() 来做这件事,Numpy 中更提供了功能更为强大的 numpy.random.choice()。然而这些东西都有一个问题,就是你必须把整个数据集读到内存里。如果数据集超出了内存的限制,或者要对一个持续的输入流做抽样,即从包含 $n$ 个项目的集合中(等概率)选取 $k$ 个样本,其中 $n$ 为很大或未知,又该怎么做呢?
素数求和的动态规划方法
怎么求出从 $2$ 到 $N$ 之间的所有素数之和?
素数求和是数论中一个很典型的问题。这事情乍听起来并不难,只要把素数都求出来再加起来就好了嘛。可能你已经了解了一些求素数的方法,比如最简单的试除。写过这个程序的同学都知道这样搞有多慢。或者常用的是埃氏筛法,简单来说,就是列好从 $2$ 到 $N$ 的范围,先用 $2$ 去筛,把从 $2 \times 2$ 开始的 2 的倍数剔掉;再用下一个素数 3 筛,把 $3 \times 3$ 开始的 3 的倍数剔除掉…… 一直筛完不大于 $\sqrt{N}$ 所有素数为止。我直接从 wiki 上借了一个动画来演示这个过程,有兴趣的同学可以自己写一个试试看。
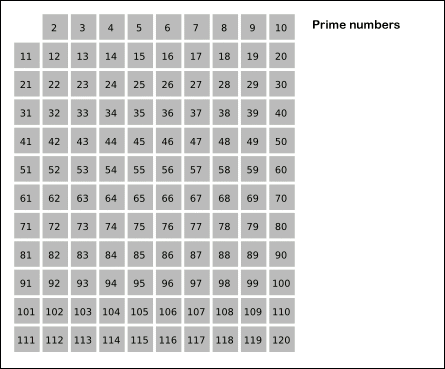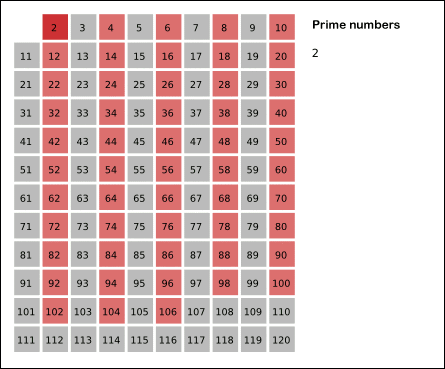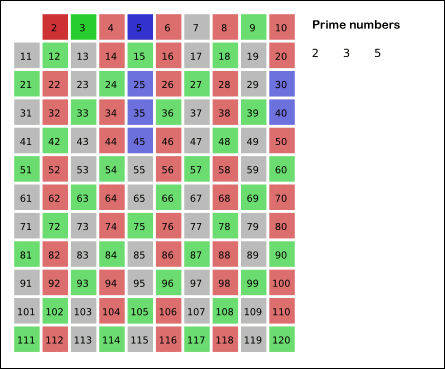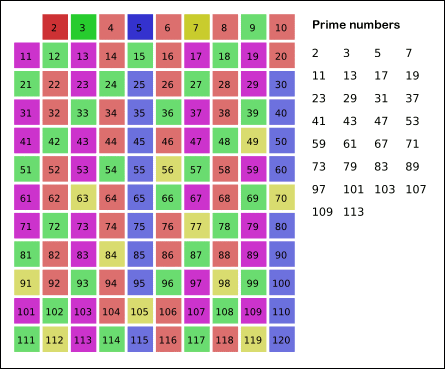
本文中的方法来自于解决了 ProjectEuler 全部问题的大神 Lucy_Hedgehog。
Continue reading “素数求和的动态规划方法”
0-1 背包问题详解 (4)
前面的方法已经非常快了,应该说很满意。那还有没有再优化的余地呢?
我们再来仔细看一下这个过程:深度优先搜索,逐级回溯,典型的二叉树遍历方式。为了方便说明,我标出了结点遍历的顺序:
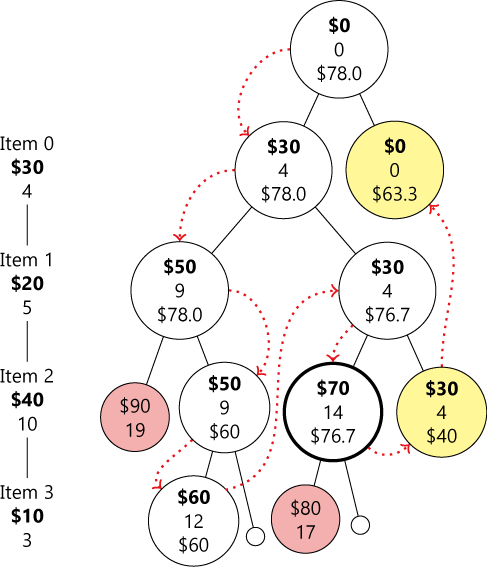
Continue reading “0-1 背包问题详解 (4)”
0-1 背包问题详解 (3)
哪能搞法——分支界限
我们先把动态规划的想法放一下,退一步来看看这个问题。每一个物品都可能放或者不放,如果用一个决策树来表示的话,就得到这样一棵满二叉树:
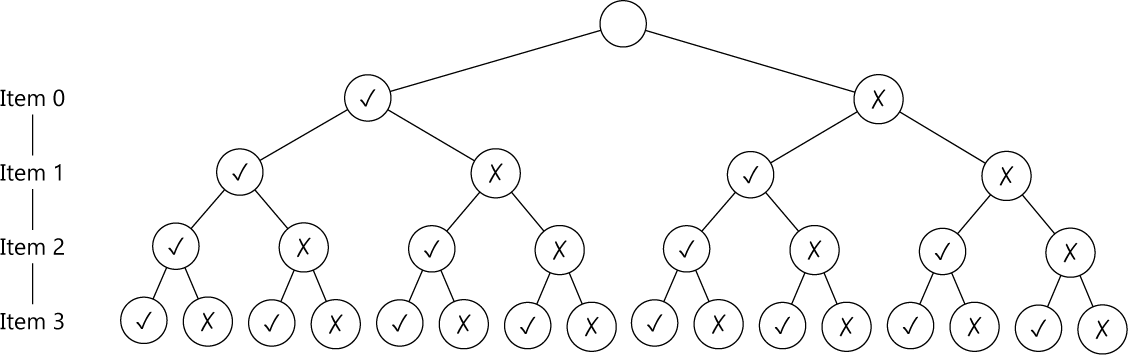
这对于 \(n\) 个物品就有 \(2^n\) 种放法,总共要计算 \(2^{n+1} – 2\) 个结点,当然是太多了。不过,有没有什么办法能让遍历的结点少一点呢?
